Pregunta 24_2010

El gráfico que representa al conjunto solución del sistema de inecuacion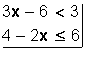es

es

Área temática: Álgebra

Comentario

El tópico que se debe saber en esta pregunta es el relacionado con sistemas de inecuaciones lineales sencillas con una incógnita. El alumno debe resolver cada una de las inecuaciones del sistema  para luego intersectar los conjuntos solución de cada una y obtener la respuesta a la pregunta.

En efecto, en la inecuación 3x ─ 6 < 3 , se suma el inverso aditivo de ─6 a cada lado de la inecuación, de donde se obtiene que

3x < 9 , luego se multiplica por el recíproco de 3 a cada lado de la inecuación, para obtener que x < 3 . El siguiente gráfico representa a todos los números reales que son menores que 3 (que no incluye al 3):

Ahora, en la inecuación 4 ─ 2x  ≤ 6 , se suma el inverso aditivo de 4 a cada lado de la inecuación, resultado ─2x  ≤ 2 , se multiplica por el recíproco de ─2 a cada lado de la inecuación, se llega a x ≥ ─1 , se debe recordar que cuando una inecuación se multiplica por un número negativo se obtiene una inecuación equivalente, donde el signo de la desigualdad cambia de sentido. El gráfico que representa esta desigualdad (que incluye el –1) es:

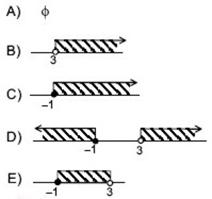
Por lo tanto, el conjunto solución para el sistema planteado es la intersección que se produce de estos dos gráficos, es decir:

Luego, la clave se encuentra en la opción E).

Esta pregunta resultó difícil y fue omitida por un alto porcentaje de alumnos. Esto se debe a que hay un dominio sólo parcial del contenido o bien a que existe un desconocimiento de éste.

El distractor más usado fue el D). El error que cometen los alumnos es, seguramente, que en la inecuación 4 ─ 2x ≤ 6 , no cambian el sentido de la desigualdad, obteniendo x ≤ ─1 y concluyen que la inecuación 3x ─ 6 < 3 es igual a ─6 ─ 3 < ─3x , obteniendo

─9 < ─3x , luego multiplican por el recíproco de ─3 a ambos lados de la inecuación sin cambiar el signo de la desigualdad llegando a 3 < x . Por último, unen los dos conjuntos soluciones en vez de intersectarlos, por lo que su representación gráfica es el distractor D).

Fuente Internet:

Publicación oficial del Demre en www.demre.cl